しんいちさんのご質問に刺激を受けてODE(Open Dynamics Engine)講座30回目を開講します。
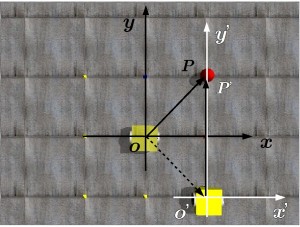
今回は相対座標系と絶対座標系の変換に関してお話しします。ODEでは相対座標系をボディ(剛体)座標系とよび、絶対座標系をワールド(世界)座標系とよびます。相互変換に関してはODE本115、116ページに説明があるのでここでは結果だけを書きます。
- 相対座標系 → 絶対座標系: dBodyGetRelPointPos()
- 絶対座標系での位置 = 回転行列 × 相対座標系の位置 + 相対座標系の原点
- 絶対座標系 → 相対座標系:dBodyGetPosRelPoint()
- 相対座標系での位置 = 回転行列の転置 × (相対座標系での位置 – 相対座標系の原点)
なお、相対座標系の原点とは絶対座標系での相対座標系の原点位置となります。ロボットの場合は相対座標系の原点をロボットの重心位置とする場合が多いです。つまり、絶対座標系でのロボットの重心位置と考えてください。
例えば、相対座標系でのあるボディの速度を計算するコードは次のようになります。
static dVector3 pos_rel; // ボールの相対位置
static dVector3 pos_rel_old; // 1ステップ前のボールの相対位置
dReal *pos_ball = (dReal *)dBodyGetPosition(ball.body);
dReal *pos_robot = (dReal *)dBodyGetPosition(robot.body);
dReal pos_tmp[3];
pos_tmp[0] = pos_ball[0]-pos_robot[0];
pos_tmp[1] = pos_ball[1]-pos_robot[1];
pos_tmp[2] = pos_ball[2]-pos_robot[2];
dMULTIPLY1_331(pos_rel, R, pos_tmp); // pos_rel = R(回転行列)の転置 × pos_tmp
dVector3 v; // ボールの相対速度
v[0] = (pos_rel[0] - pos_rel_old[0])/step_size; // step_sizeはdWorldStep()の2番目の引数 v[1] = (pos_rel[1] - pos_rel_old[1])/step_size;
v[1] = (pos_rel[1] - pos_rel_old[1])/step_size;
v[2] = (pos_rel[2] - pos_rel_old[2])/step_size;
pos_rel_old[0] = pos_rel[0];
pos_rel_old[1] = pos_rel[1];
pos_rel_old[2] = pos_rel[2];
dBodyGetPosRelPoint()を使うと次のように簡単になります。
static dVector3 pos_rel; // ボールの相対位置 static dVector3 pos_rel_old; // 1ステップ前のボールの相対位置 dReal *pos_ball = (dReal *)dBodyGetPosition(ball.body); dVector3 pos_rel; dBodyGetPosRelPoint(robot.body, pos_ball[0], pos_ball[1], pos_ball[2], pos_rel) dVector3 v; // ボールの相対速度 v[0] = (pos_rel[0] - pos_rel_old[0])/step_size; v[1] = (pos_rel[1] - pos_rel_old[1])/step_size; v[2] = (pos_rel[2] - pos_rel_old[2])/step_size; pos_rel_old[0] = pos_rel[0]; pos_rel_old[1] = pos_rel[1]; pos_rel_old[2] = pos_rel[2];
なお、ODEでは次に紹介する相対座標系と絶対座標系に関する便利なAPI達がいます。ソースコードも掲載していますので参考にしてください。
// posr.pos: ボディ参照点の絶対座標系での位置
// posr.R: ボディ参照点の絶対座標系での回転行列
// 相対座標系の位置(px, py, pz)を絶対座標系に変換する
void dBodyGetRelPointPos (dBodyID b, dReal px, dReal py, dReal pz, dVector3 result)
{
dVector3 prel, p;
prel[0] = px; prel[1] = py; prel[2] = pz; prel[3] = 0;
dMULTIPLY0_331 (p,b->posr.R, prel); // 行列の掛け算 p = b->posr.R × prel
result[0] = p[0] + b->posr.pos[0];
result[1] = p[1] + b->posr.pos[1];
result[2] = p[2] + b->posr.pos[2];
}
// 絶対座標系の位置(px, py, pz)を相対座標系に変換する。
// dBodyGetRelPointPosの反対。
void dBodyGetPosRelPoint (dBodyID b, dReal px, dReal py, dReal pz, dVector3 result)
{
dVector3 prel;
prel[0] = px - b->posr.pos[0]; // ボディ座標系の位置
prel[1] = py - b->posr.pos[1];
prel[2] = pz - b->posr.pos[2];
prel[3] = 0;
dMULTIPLY1_331 (result, b->posr.R, prel);
}
// ボディ座標系で表されている位置(px, py, pz)の速度を絶対座標系で取得する。
void dBodyGetRelPointVel (dBodyID b, dReal px, dReal py, dReal pz, dVector3 result)
{
dVector3 prel,p;
prel[0] = px; prel[1] = py; prel[2] = pz; prel[3] = 0; // ボディ座標系の位置
dMULTIPLY0_331 (p, b->posr.R, prel); // ボディ座標系を絶対座標系に変換
result[0] = b->lvel[0]; // b->lvel 参照点の速度
result[1] = b->lvel[1];
result[2] = b->lvel[2];
dCROSS (result,+=,b->avel, p); // b->avel 参照点の角速度, dCROSS 外積
}
//絶対座標系で表されている位置(px, py, pz)の速度を絶対座標系で取得する。
void dBodyGetPointVel (dBodyID b, dReal px, dReal py, dReal pz, dVector3 result)
{
dVector3 p;
p[0] = px - b->posr.pos[0];
p[1] = py - b->posr.pos[1];
p[2] = pz - b->posr.pos[2];
p[3] = 0;
result[0] = b->lvel[0];
result[1] = b->lvel[1];
result[2] = b->lvel[2];
dCROSS (result,+=,b->avel,p);
}
// 相対座標系のベクトルを絶対座標系に変換
void dBodyVectorToWorld (dBodyID b, dReal px, dReal py, dReal pz,dVector3 result)
{
dVector3 p;
p[0] = px; p[1] = py; p[2] = pz; p[3] = 0;
dMULTIPLY0_331 (result,b->posr.R,p); // 回転行列Rにベクトルpを掛ける
}
// 絶対座標系のベクトルを相対座標系に変換
void dBodyVectorFromWorld (dBodyID b, dReal px, dReal py, dReal pz, dVector3 result)
{
dVector3 p;
p[0] = px; p[1] = py; p[2] = pz; p[3] = 0;
dMULTIPLY1_331 (result,b->posr.R,p); // 回転行列Rの転置にベクトルpを掛ける
}
また、次回よろしくね。

コメント