12. Friction

This is the 12th ODE (Open Dynamics Engine) tutorial.

This tutorial explains a friction. Many people have already learned the friction in high school. The friction model is the following equation.

| fT | <= μ | fN |

Where, fN is the normal direction,  fT is a tangential force vector, and  μ is the coefficient of friction. The equation express the friction cone,  fN vector is an axis of the cone and the vertex is the contact point.  If the composed vector of fT and fN is inside the friction cone, there is no slip at the contact point.  Slip is occered if the composed vector is outside of the friction cone.

ODE adopts approximaitons of the coulomb friction model. ODE has two models, such as the constant force limit model and the friciton pyramid approximation model. The default model is the constant force limit model. Please select the friction pyramid approximation model, if collisions between an object and the groud are very important for the simulation.

1. Constant force limit
The  coefficient of friction  μ　is modeled as of the maximum friction model. This is not accuraty physics model, it is, however, computationl cost is the lowest.

2. Friction pyramid approximation
The friction cone is modeled as the friction pyramid. This model is more accurate compared than the constant force limit. If you want to use this model, you must set the dContactApprox1 flag.

The following program shows how to set the friction model. In line 17, if a geometry is box[0].geom , the dContactApprox1 flag is set.  Otherwise, the contant force limit modes is adpoted.

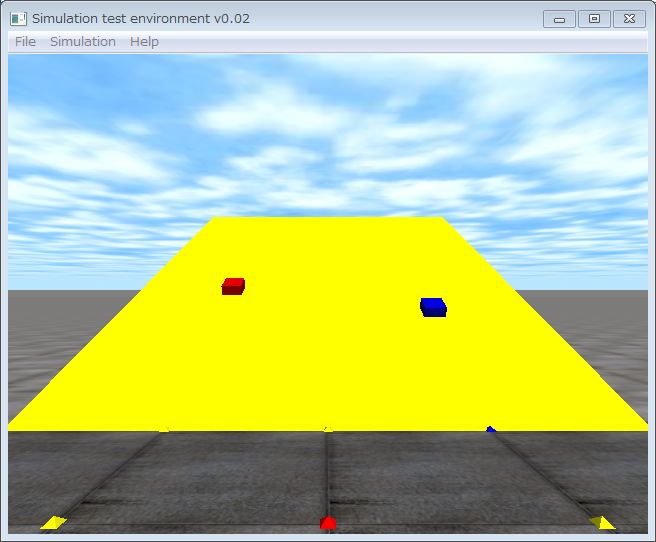
In the sample program, gradually increasing the angle of the slope, the two boxes begin to slip at the different angle. Coefficient of friction is set to 1, so, thoretically the box begins to slide at 45 degree. The friction pyramid approximate model (the red box on the left) begins to slip at about 45 degrees, and the contact force limit model begins to slip more low angle.

You can download the sample program, sample12.cpp (sample12-110105.zip), from here. Please try and enjoy it.

static void nearCallback(void *data, dGeomID o1, dGeomID o2)
{
  const int N = 10;
  dContact contact[N];
  if (((o1 == ground) && (o2 == slope )) ||  ((o1 == slope)  && (o2 == ground))) return;

  int isGround = ((ground == o1 || slope == o1)  || (ground == o2 || slope == o2));
  int n =  dCollide(o1, o2, N, &contact[0].geom, sizeof(dContact));

  if (isGround)  {
    for (int i = 0; i < n; i++) {
      if ((o1 == box[0].geom) || (o2 == box[0].geom)) {
         // friciton: friction pyramid model
         contact[i].surface.mode = dContactApprox1|dContactSoftERP|dContactSoftCFM;
      }
      else {
         // friction: constant force limit model　
         contact[i].surface.mode = dContactSoftERP|dContactSoftCFM;
      }

      contact[i].surface.mu   = 1.0; // dInfinity;
      contact[i].surface.soft_erp = 1.0; //1.0;
      contact[i].surface.soft_cfm = 1e-10;
      dJointID c = dJointCreateContact(world, contactgroup, &contact[i]);
      dJointAttach(c,dGeomGetBody(contact[i].geom.g1), dGeomGetBody(contact[i].geom.g2));
    }
  }
}

That’s all. See you !

demu